Example 4: Approximate MIMO data transfer using input-output normalization

Problem description

Let us be given a MIMO input-output frequency-domain data set, the objective is to find an exact (stable) interpolating model. As an additional objective, one wants that all tranfers are equally reproduced, independently of their magnitude. Let us define the MIMO random stable system and evaluate its transfer function response.

% Random 100-states 2 inputs 1 output model and frequency evaluation
rng(1234,'twister');
sys        = stabsep(rss(100,1,2)); % let remove the unstable part
sys.b(:,1) = sys.b(:,1)*1e5; % the first input gain is artificially amplified
W          = logspace(-1,2,200);
H          = freqresp(sys,W);

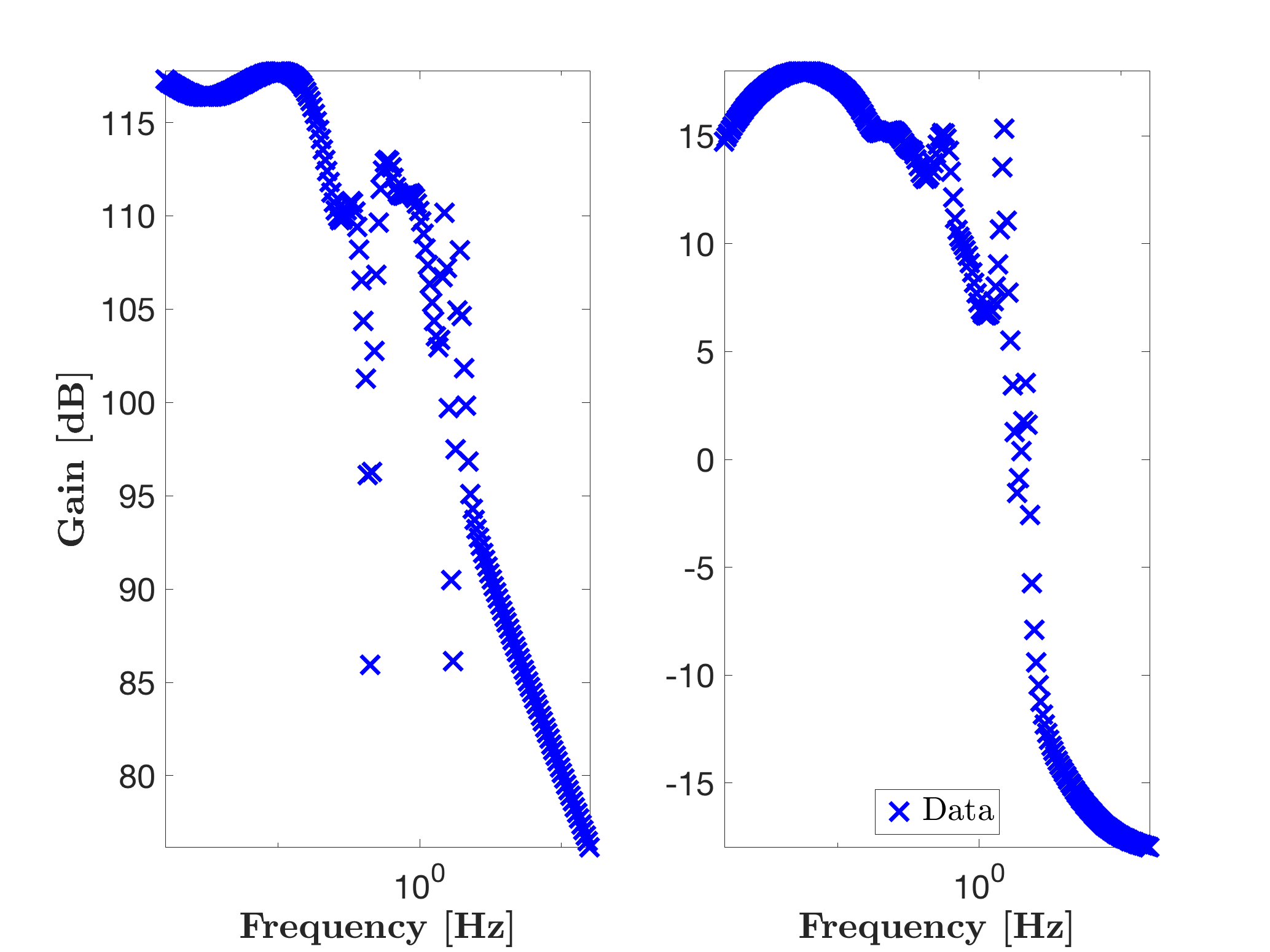
figure
mor.bode({H},'bx',W);
legend('Data','Location','South')

One obtains the following frequency responses. Note that the first input gain is much larger than the second one.

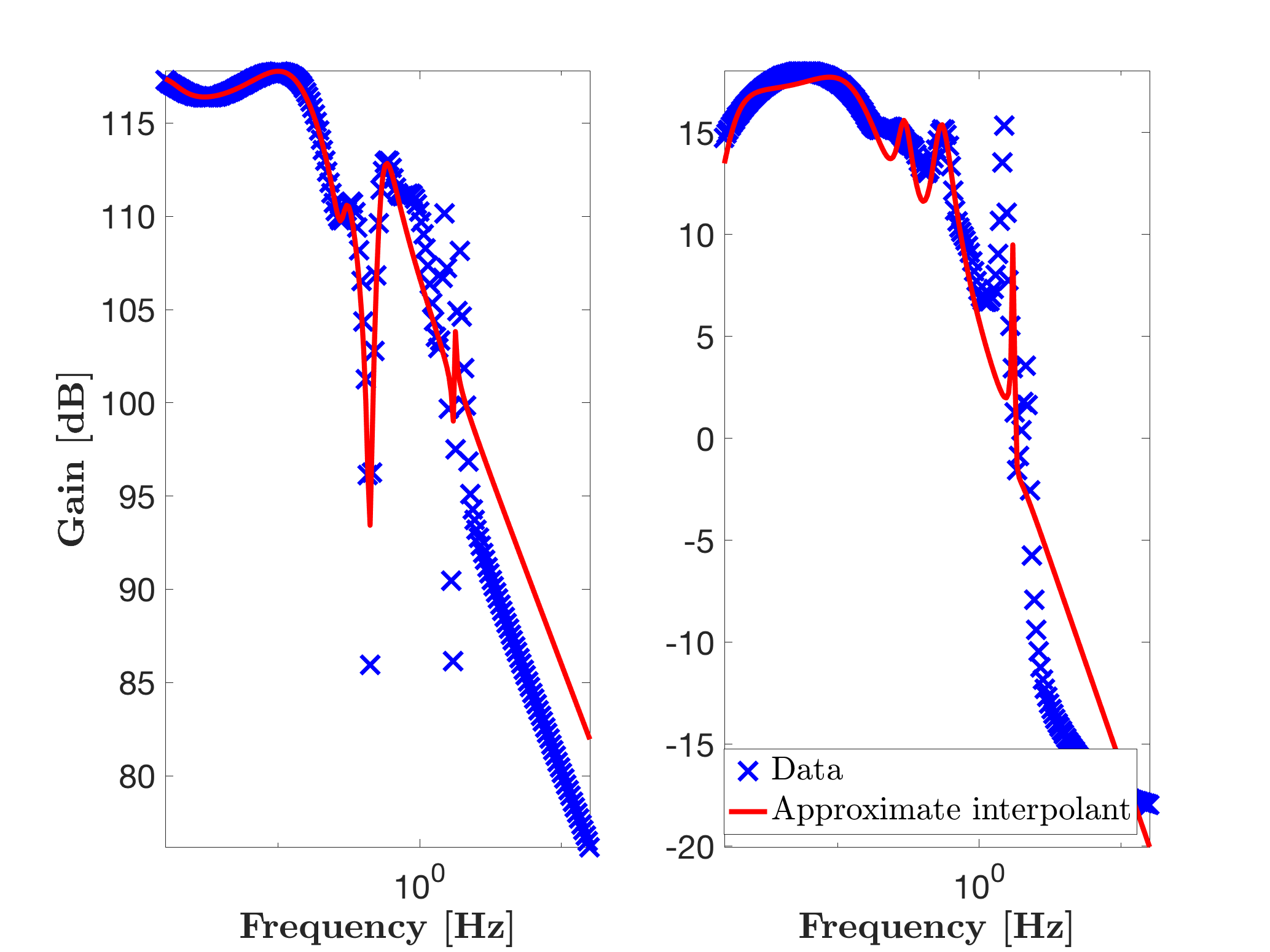
Invoking mor.lti, with approximation order objective r = 10, as follows:

% Exact interpolation
r             = 10;
[sysr1,info1] = mor.lti({W,H},r);

hold on
mor.bode(sysr1,'r-',W);
legend('Data','Exact interpolant','Location','South')

leads to the model sysr1 of order 10. Note that the first transfer is well catched while the second one, quite badly reproduced...

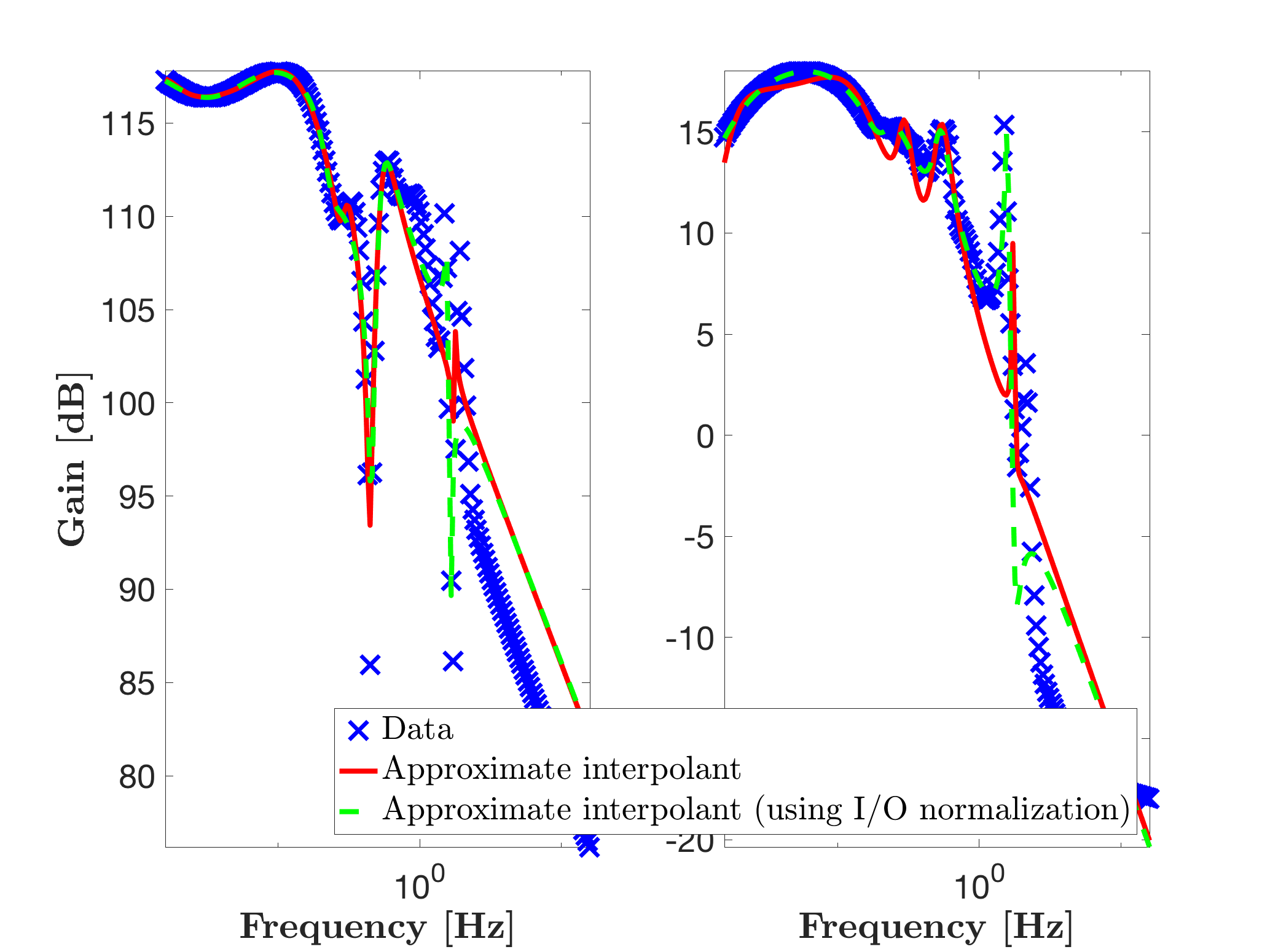
Now, let us scale the input output gains using the opt.ioNormalize = true, with the same approximation order as follows:

% Exact interpolation with input-output normalization
opt.ioNormalize = true;
[sysr2,info2]   = mor.lti({W,H},r,opt);

hold on
mor.bode(sysr2,'g-',W);
legend('Data','Exact interpolant','Exact interpolant (using I/O normalization)','Location','South')

leads to the model sysr2 which clearly equally reproduces the two transfer, whatever the amplitude are.