Example 2: Simplify a very large-scale model

Problem description

Let us be given a state-space model described by a very large-scale DAE matrix set, the objective is to find an approximate reduced order model, using different options and features of the MOR Toolbox. As the considered problem involves a potentially very large-scale model, the sparsity of the dynamical matrices is now exploited. Let us get the state-space model from the Oberwolfach library, standardly used in large-scale problems. Then, using the mmread function from Matrix Market Matlab function page, one can extract the sparse A, B, C, D and E matrices. In the considered exmaple, we used the T2DAH use case (download the Matrix Market link).

% Obtain a sparse state-space test model from the Oberwolfach web page
% Extract A, B, C, D, E matrices using mmread.m function from Matrix Market
W = logspace(-2,2,50);
r = 10;
D = zeros(size(C,1),size(B,2));

% Reduce it using ITIA (which fully exploits sparsity properties)
opt.method   = 'itia';
opt.verbose  = true;
[sysr,info1] = mor.lti({A,B,C,D,E},r,opt);

figure
mor.bode({A,B,C,D,E},'b-',sysr,'r--',W);
legend(['Original, n=' num2str(length(A))],['Approximated, r=' num2str(r)],'Location','South')

One obtains the following frequency responses of the original and approximated models.

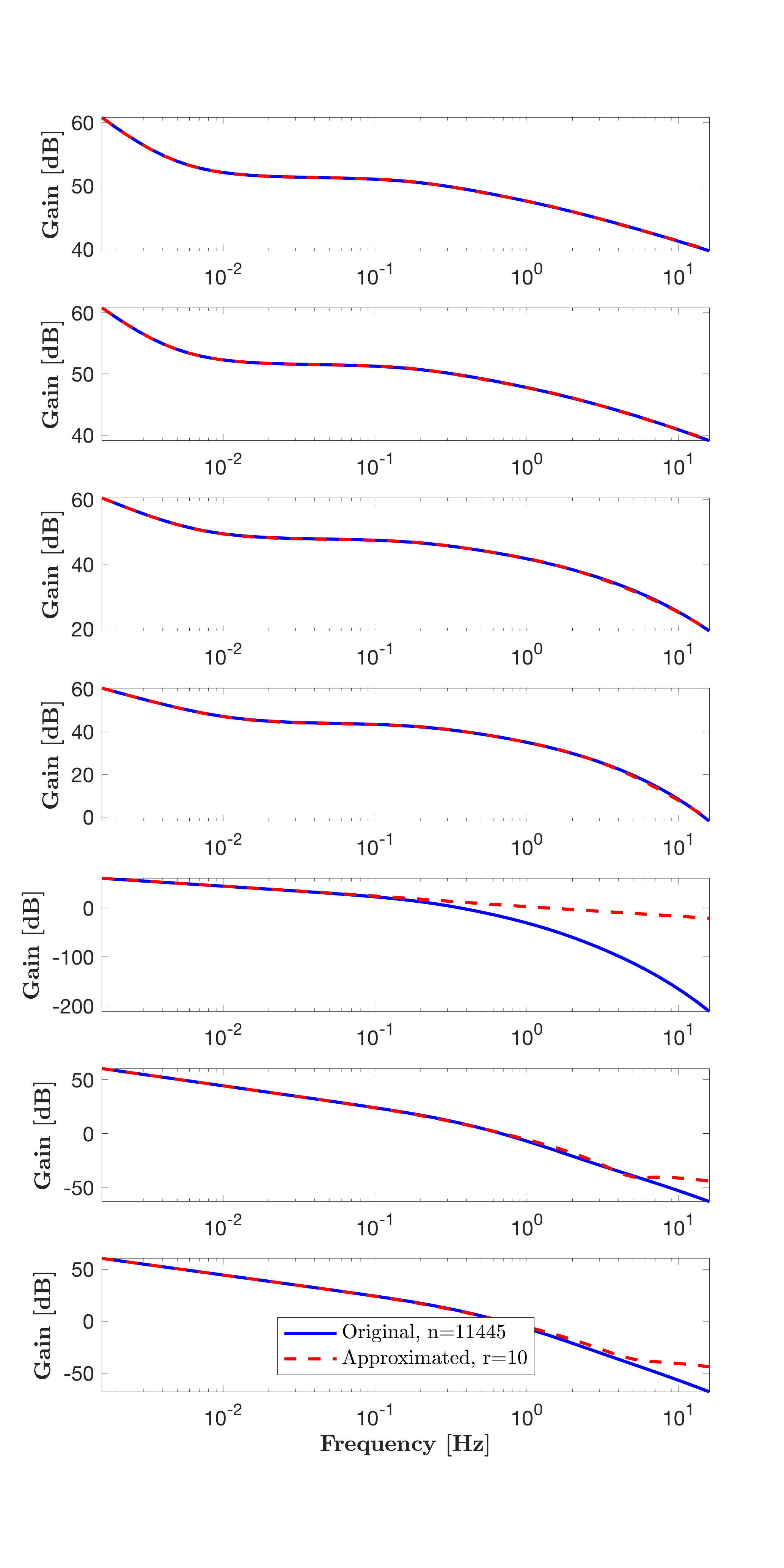
Clearly, the approximated model of dimension 10 well reproduces the original one of dimension 11,445. Moreover, one may notice that the solution is obtained in few seconds, as the method fully exploits the sparsity property of the matrix set.