La suite MDS est composée de deux produits: la librairie MDSPACK et la boîte à outils MOR.
Ces deux outils complémentaires et non-intrusifs peuvent être utilisés pour traiter une large variété de problèmes. Ils visent à accompagner et à faciliter le travail des techniciens, ingénieurs et chercheurs dans la manipulation des systèmes dynamiques et des tenseurs de données, c'est à dire leur modélisation, simulation, analyse, contrôle ou optimisation.
La suite MDS est utilisée dans différents domaines applicatifs: aéronautique, canaux hydro-électriques, climatologie, spatial, physique des structures et des fluides, systèmes biologiques... Quelques applications sont succinctement présentées ici.
Librairie MDSPACK
MDSPACK est une librairie Fortran compilée, interfacée avec MATLAB®, Python, et l'interface de ligne de commande. Elle fournit des algorithmes avancés permettant
- d'approximer des modèles dynamiques linéaires de dimension finie et infinie,
- d'identifier des modèles dynamiques linéaires d'ordre réduit, à partir de données fréquentielles ou temporelles,
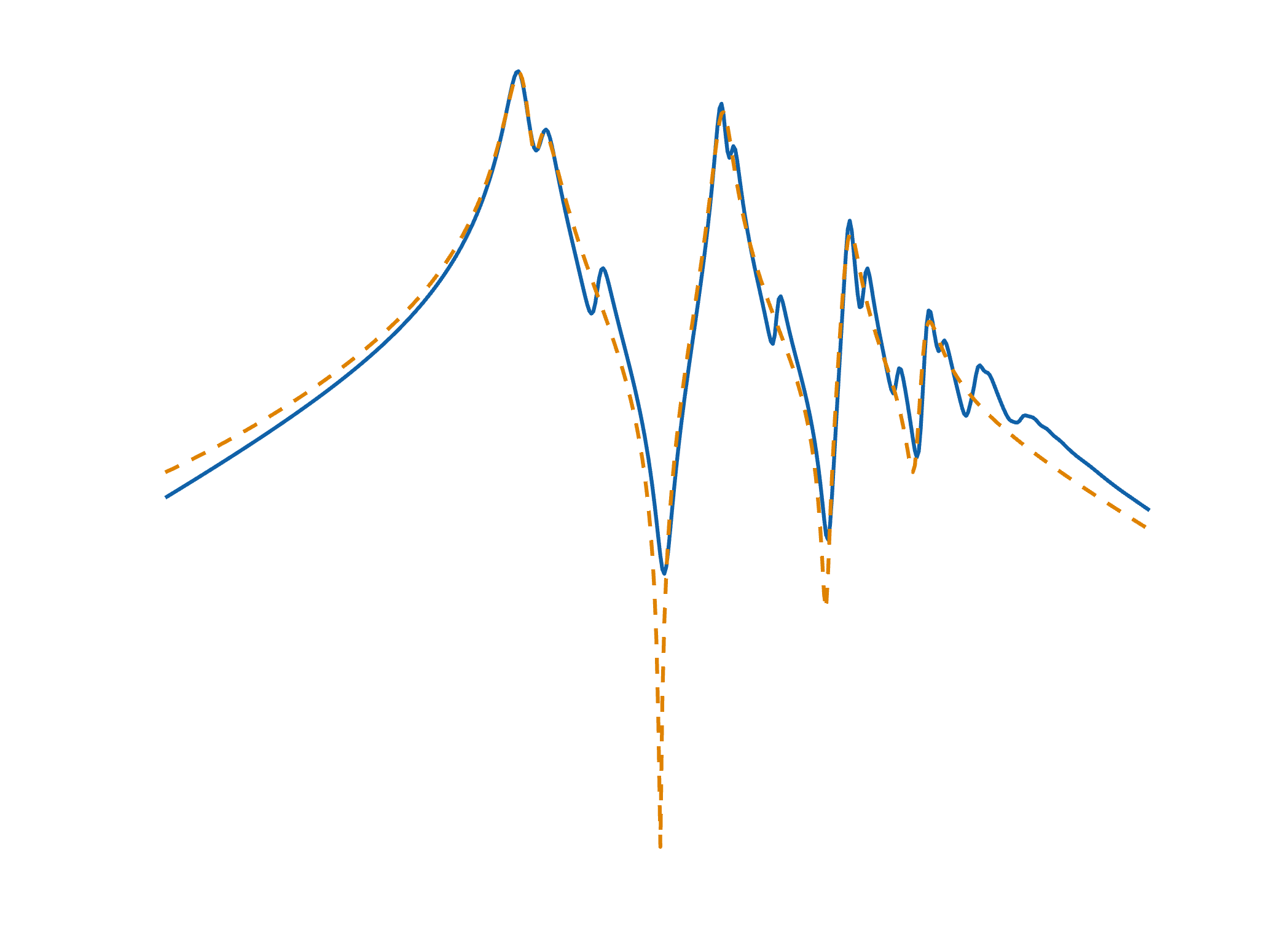
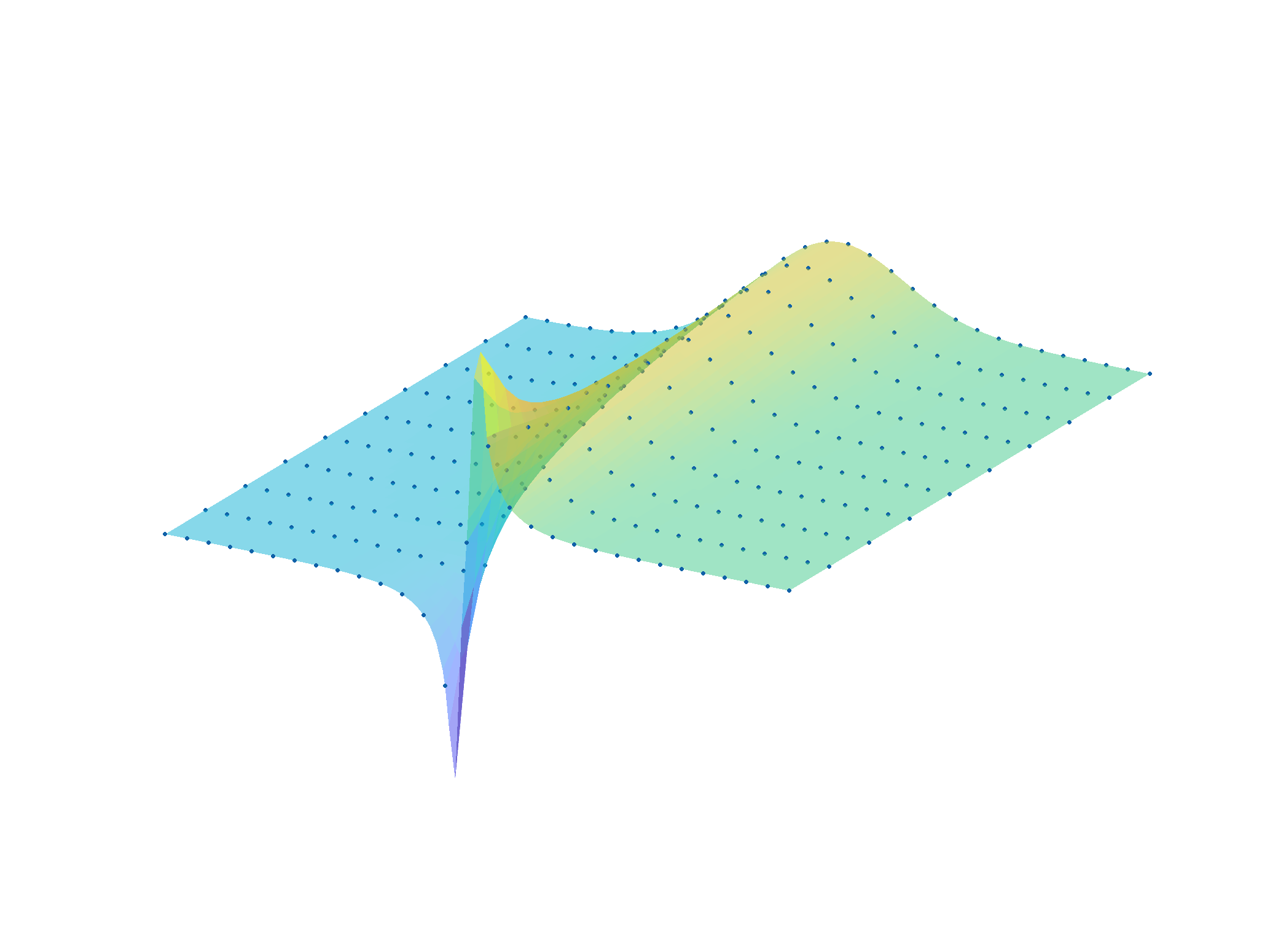
- d'approximer des grands tenseurs de données par des fonctions rationnelles multi-variées (dynamiques ou statiques), et
- d'analyser des modèles de grande dimension ou de dimension infinie (e.g. normes, stabilité, ...).
Afin de s'adapter et d'optimiser votre processus et problème de modélisation, de réduction et d'approximation, un large panel de fonctions et d'options sont proposés.
Librairie MDSPACK
Identification, approximation et analyse des systèmes dynamiques et des tenseurs
Boîte à outils MOR
MOR est une boîte à outils basée sur MATLAB®. Elle fournit des algorithmes permettant
- de réduire des modèles dynamiques linéaires de grande dimension, et
- de construire des modèles dynamiques linéaires à partir de données fréquentielles.
Les algorithmes de la boîte à outils MOR génèrent un modèle sous forme de représentation d'état linéaire dont le comportement entrées/sorties est proche de celui du modèle initial.
Essayer ou acheter

La suite MDS est gratuite pour une utilisation académique.

Différentes licences sont disponibles pour les professionnels.

Des questions, des besoins spécifiques? Contactez-nous.