The MDS suite is composed of two products: the MDSPACK library and the MOR toolbox.

These two complementary and non-intrusive tools may be used to treat a large variety of problems and use-cases. The main objective is to accompany and ease the work of technicians, engineers and researchers in the manipulation of dynamical systems and data tenors, and more sepcifically their modelling, simulation, analysis, control or optimisation.

The MDS suite is already used in different applicative domains including: aeronautics, hydro-electrical open channels, climatology, space systems, physics of structures and fluids, biological systems... Some applications are briefly presented here.

MDSPACK is a Fortran compiled library, interfaced with MATLAB^®, Python, and the command line interface. It provides advanced functions allowing

• to approximate finite and infinite dimensional linear dynamical models,
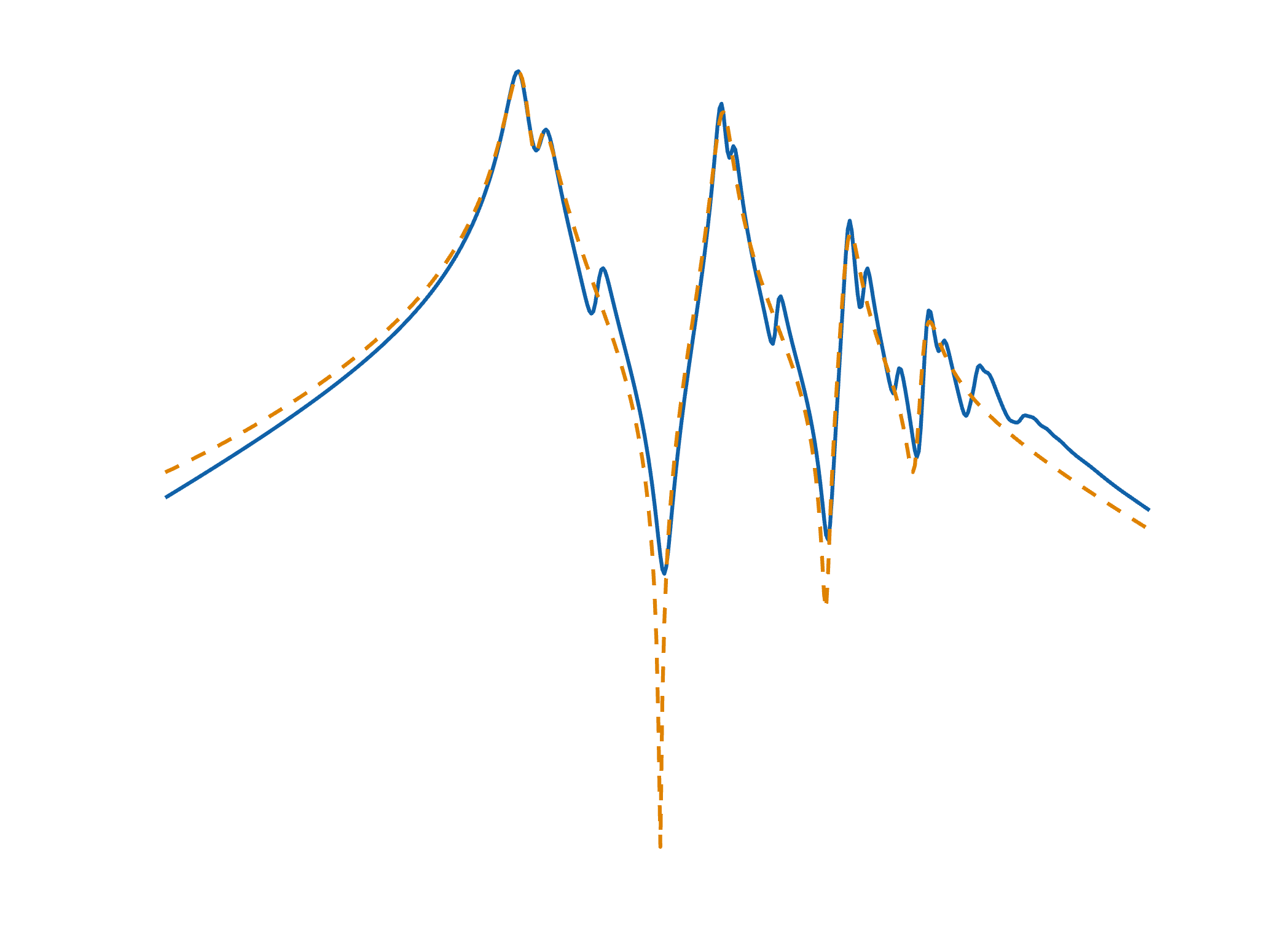
• to identify reduced order linear dynamical models, directly from frequency or time-domain data,
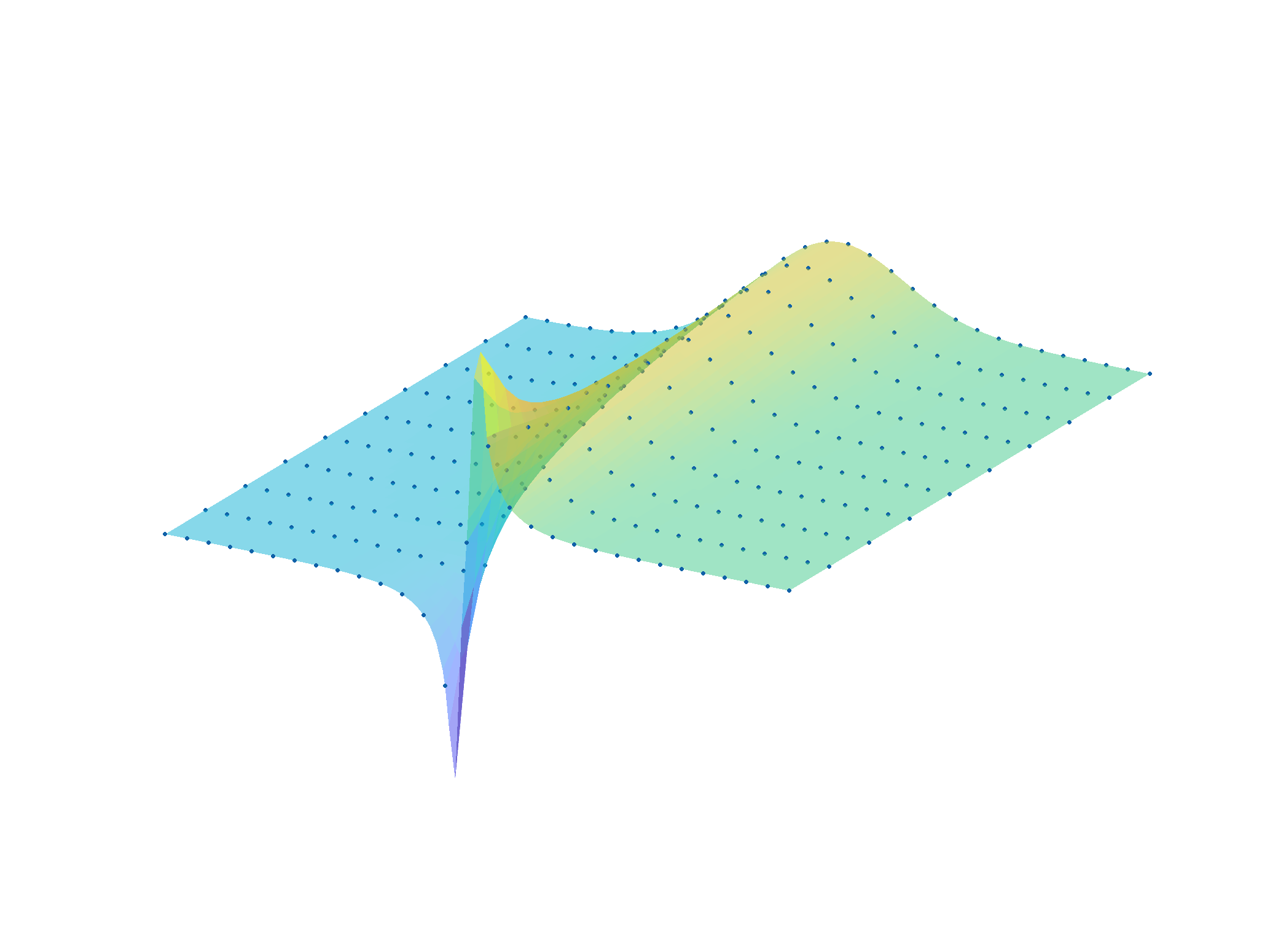
• to approximate large dimensional tensors by (dynamical or static) multivariate rational functions, and
• to analyse properties of large-scale and infinite dimensional models (e.g. norms, stability, ...).

In order to fit and optimize your specific modelling, reduction and approximation problem, a bundle of functions and options are proposed.

MOR is a MATLAB^® based toolbox. It provides advanced functions allowing

• to reduce large-scale linear dynamical models, and
• to construct linear dynamical models from frequency-domain data.

The MOR toolbox functions generate a linear dynamical model in state-space form which input/output behaviour is close to the original one.