Problem statement

Let us consider a set of frequency-domain data 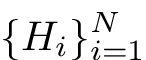, describing the multiple-input multiple-output (MIMO) system transfer responses at frozen pulsations as

.

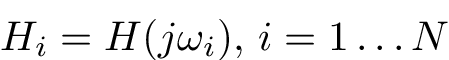Then, the objective is to construct a MIMO LTI model that either exactly interpolates the data (with dimension of minimal order 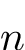) or well approximate them (with dimension of order ).

Warning: approximation is not necessarily reduction

This objective is slightly different from the model reduction one that considers an internal state dimensionality reduction. Here instead, given some discrete data, one seeks a LTI model that approximates them. This objective is in some sense close to the identification problem, but attacked from a different viewpoint, known as the interpolation problem. With respect to model reduction, here one talk of model approximation instead.

Approximation interface

Let the data be represented by the variable sys = {w_i,H_i}, gathering the N pulsations and the corresponding nu inputs, ny outputs responses given as:

• w_i, a vector of positive pulsations of dimension N x 1 and
• H_i, a ny x nu x N matrix which index H_i(i,j,k) represents the i-th output, j-th input, k-th pulsation response of the system (i=1...ny, j=1...nu and k=1...N).

The LTI approximating / interpolating model (sysr), an ODE / DAE model of order (r), can then be obtained through the unified reduction interface mor.lti as follows:

where the structure opt enables to specify the reduction options which are detailled on the mor.lti page. This method allows to either exactly match the data or perform an approximate interpolation.

Examples and how to

Perform a first data-driven rational interpolation

Exact or approximate rational interpolation from input-output data.

Approximate data over a frequency-limited band

Perform data-driven model approximation over a frequency-limited frequency range.

Approximate data while enforcing model stability

Approximate the data while enforcing the approximating model stability.

Approximate MIMO data transfer using input-output normalization

Approximate the data independently from their magnitude, in a eye ball fashion, using input-output scaling.

Approximate transfer from a time-domain simulator

Given a time-domain simulator, obtain an approximation the transfer function.